Inertial Tensors and Mass Properties for the BarrettHand BH8-280

The inertial properties calculated here represent the masses and inertias of each link of the BarrettHand BH8-280. All calculations were made using SolidWorks 2012 SP 3.0 and CAD models that include all mechanical components of the hand (including fasteners) and all electrical components except wiring. To verify that the SolidWorks model was correct, assemblies and parts of an actual hand were massed for comparison.

The mass of an actual finger was measured at 179 g, which matches the mass of the CAD model. The hand base (including pucks and finger motors) measured 664 g while SolidWorks calculated the mass of the CAD model to be only 643 g. This discrepancy could come from a number of sources:

1. Lack of wiring in CAD
2. Lack of grease in CAD
3. Inadequately modeled PCB and components

Further investigation narrowed the source of error to electrical subassemblies with dozens of strands of wire, all of which were omitted in the CAD model. To replicate the mass of these wires, slugs of the missing mass were created to fill the cavities in which wires could run. The base CAD model used in the calculations below measures 664 g.

In the following images, all parts are left transparent to display all parts of the mass calculations. Yellow denotes frame parts, red denotes electrical pieces, and blue is for motors and drivetrain components.

The following inertial frames are established on the hand. In each of the following diagrams, coordinate systems are oriented with the Z-axis coincident to the axis of rotation of each joint. These inertial frames follow the same convention as on the BarrettHand BH8-262.

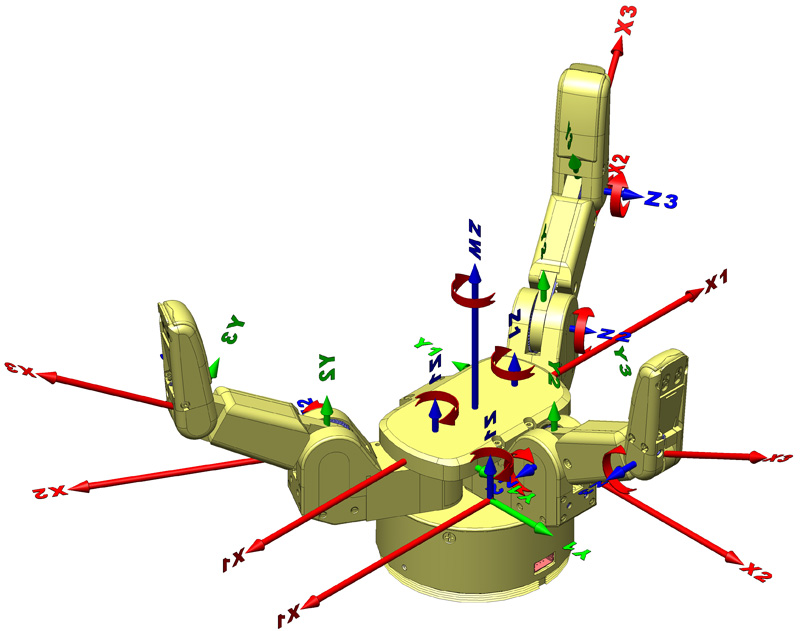
Since no one is likely to wish to attempt computed-torque control on the Hand axes (since the frictions in the Hand are very high), the backdriven, reflected drive inertias of the drives were not computed. Since backdriven drive inertias have no effect on gravity terms, the frame inertias should give you good results for controlling the WAM arm and wrist torques as functions of hand-finger positions.

You may also view mass properties of the entire hand in various configurations here: ​http://web.barrett.com/support/BarrettHand_Documentation/BarrettHand280MassProp-2010Dec10.pdf

Mass Properties for Frame W (hand base frame) with palm pad

Output coordinate System: Frame W (opaque)

Mass = 0.60858 kilograms

Volume = 0.00024871 cubic meters

Surface area = 0.24908 square meters

Center of mass: (meters)

X = 5.0019e-005 Y = -0.0044561 Z = 0.037268

Principal axes of inertia and principal moments of inertia: (kilograms * square meters) Taken at the center of mass.

Ix = (0.0025349, 0.91612, -0.4009)	Px = 0.00047536
Iy = (0.012636, -0.40089, -0.91604)	Py = 0.0006507
Iz = (-0.99992, -0.0027435, -0.012592)	Pz = 0.00069861

Moments of inertia: (kilograms * square meters) Taken at the center of mass and aligned with the output coordinate system.

Lxx = 0.0006986	Lxy = 2.7577e-007	Lxz = -7.8138e-007
Lyx = 2.7577e-007	Lyy = 0.00050354	Lyz = -6.44e-005
Lzx = -7.8138e-007	Lzy = -6.44e-005	Lzz = 0.00062253

Moments of inertia: (kilograms * square meters) Taken at the output coordinate system.

Ixx = 0.001556	Ixy = 1.4013e-007	Ixz = 3.5309e-007
Iyx = 1.4013e-007	Iyy = 0.0013488	Iyz = -0.00016547
Izx = 3.5309e-007	Izy = -0.00016547	Izz = 0.00063461

Mass Properties for Frame W (hand base frame) without palm pad

Output coordinate System: Frame W (opaque)

Mass = 0.59573 kilograms

Volume = 0.00023933 cubic meters

Surface area = 0.23262 square meters

Center of mass: (meters)

X = 5.1098e-005 Y = -0.0050433 Z = 0.036671

Principal axes of inertia and principal moments of inertia: (kilograms * square meters) Taken at the center of mass.

Ix = (0.0027331, 0.90166, -0.43244)	Px = 0.00045391
Iy = (0.01699, -0.43242, -0.90151)	Py = 0.00063852
Iz = (-0.99985, -0.0048831, -0.016501)	Pz = 0.00067156

Moments of inertia: (kilograms * square meters) Taken at the center of mass and aligned with the output coordinate system.

Lxx = 0.00067154	Lxy = 2.9365e-007	Lxz = -7.6321e-007
Lyx = 2.9365e-007	Lyy = 0.00048844	Lyz = -7.1984e-005
Lzx = -7.6321e-007	Lzy = -7.1984e-005	Lzz = 0.00060401

Moments of inertia: (kilograms * square meters) Taken at the output coordinate system.

Ixx = 0.0014878	Ixy = 1.4013e-007	Ixz = 3.5309e-007
Iyx = 1.4013e-007	Iyy = 0.0012896	Iyz = -0.00018216
Izx = 3.5309e-007	Izy = -0.00018216	Izz = 0.00061916

Mass Properties for Frame 1 (finger spread frame)

Output coordinate System: F1 (opaque)

Mass = 0.14109 kilograms

Volume = 3.919e-005 cubic meters

Surface area = 0.058268 square meters

Center of mass (meters):

X = 0.030616 Y = -7.3219e-005 Z = -0.011201

Principal axes of inertia and principal moments of inertia (kilograms * square meters), taken at the center of mass:

Ix = (-0.99149, -0.0047957, -0.13013)	Px = 1.9838e-005
Iy = (0.13011, 0.0033343, -0.99149)	Py = 6.904e-005
Iz = (0.0051888, -0.99998, -0.0026819)	Pz = 7.4106e-005

Moments of inertia (kilograms * square meters), taken at the center of mass and aligned with the output coordinate system:

Lxx = 2.0672e-005	Lxy = 2.6024e-007	Lxz = 6.3481e-006
Lyx = 2.6024e-007	Lyy = 7.4105e-005	Lyz = 1.7118e-008
Lzx = 6.3481e-006	Lzy = 1.7118e-008	Lzz = 6.8207e-005

Moments of inertia (kilograms * square meters), taken at the output coordinate system:

Ixx = 3.8374e-005	Ixy = -5.604e-008	Ixz = -4.2034e-005
Iyx = -5.604e-008	Iyy = 0.00022405	Iyz = 1.3283e-007
Izx = -4.2034e-005	Izy = 1.3283e-007	Izz = 0.00020045

Mass Properties for Frame 2 (finger inner link frame) without fingertip torque sensor

Output coordinate System: F2_Origin

Mass = 0.05832 kilograms

Volume = 1.629e-005 cubic meters

Surface area = 0.026068 square meters

Center of mass (meters):

X = 0.022042 Y = 0.00082603 Z = 0.0005526

Principal axes of inertia and principal moments of inertia (kilograms * square meters), taken at the center of mass:

Ix = (-0.99971, -0.016746, 0.017324)	Px = 4.7372e-006
Iy = (0.016611, -0.99983, -0.007873)	Py = 4.1939e-005
Iz = (0.017453, -0.0075829, 0.99982)	Pz = 4.3077e-005

Moments of inertia (kilograms * square meters), taken at the center of mass and aligned with the output coordinate system:

Lxx = 4.7592e-006	Lxy = 6.2295e-007	Lxz = -6.6417e-007
Lyx = 6.2295e-007	Lyy = 4.1929e-005	Lyz = -2.1644e-009
Lzx = -6.6417e-007	Lzy = -2.1644e-009	Lzz = 4.3066e-005

Moments of inertia (kilograms * square meters), taken at the output coordinate system:

Ixx = 4.8168e-006	Ixy = 1.6848e-006	Ixz = 4.6191e-008
Iyx = 1.6848e-006	Iyy = 7.0281e-005	Iyz = 2.4457e-008
Izx = 4.6191e-008	Izy = 2.4457e-008	Izz = 7.144e-005

Mass Properties for Frame 2 (finger inner link frame) with fingertip torque sensor

Output coordinate System: F2_Origin

Mass = 0.062139 kilograms

Volume = 1.7634e-005 cubic meters

Surface area = 0.028654 square meters

Center of mass (meters):

X = 0.023133 Y = 0.00078642 Z = 0.00052792

Principal axes of inertia and principal moments of inertia (kilograms * square meters), taken at the center of mass:

Ix = (-0.99972, -0.015048, 0.018278)	Px = 4.7942e-006
Iy = (0.014917, -0.99986, -0.0073066)	Py = 4.3325e-005
Iz = (0.018386, -0.0070319, 0.99981)	Pz = 4.4454e-005

Moments of inertia (kilograms * square meters), taken at the center of mass and aligned with the output coordinate system:

Lxx = 4.8162e-006	Lxy = 5.7981e-007	Lxz = -7.2483e-007
Lyx = 5.7981e-007	Lyy = 4.3317e-005	Lyz = -2.6653e-009
Lzx = -7.2483e-007	Lzy = -2.6653e-009	Lzz = 4.4441e-005

Moments of inertia (kilograms * square meters), taken at the output coordinate system:

Ixx = 4.872e-006	Ixy = 1.7103e-006	Ixz = 3.4041e-008
Iyx = 1.7103e-006	Iyy = 7.6588e-005	Iyz = 2.3133e-008
Izx = 3.4041e-008	Izy = 2.3133e-008	Izz = 7.7733e-005

Mass Properties for Frame 3 (fingertip frame) without fingertip pressure pad

Output coordinate System: F3 (opaque)

Mass = 0.041377 kilograms

Volume = 1.5627e-005 cubic meters

Surface area = 0.019684 square meters

Center of mass (meters):

X = 0.022825 Y = 0.0010491 Z = 0.00042038

Principal axes of inertia and principal moments of inertia (kilograms * square meters), taken at the center of mass:

Ix = (-0.99921, -0.032055, 0.023536)	Px = 3.0842e-006
Iy = (0.023767, -0.0068431, 0.99969)	Py = 1.568e-005
Iz = (-0.031884, 0.99946, 0.0075995)	Pz = 1.6826e-005

Moments of inertia (kilograms * square meters), taken at the center of mass and aligned with the output coordinate system:

Lxx = 3.1053e-006	Lxy = 4.3996e-007	Lxz = -2.9595e-007
Lyx = 4.3996e-007	Lyy = 1.6812e-005	Lyz = -1.8205e-008
Lzx = -2.9595e-007	Lzy = -1.8205e-008	Lzz = 1.5673e-005

Moments of inertia (kilograms * square meters), taken at the output coordinate system:

Ixx = 3.1582e-006	Ixy = 1.4308e-006	Ixz = 1.0106e-007
Iyx = 1.4308e-006	Iyy = 3.8376e-005	Iyz = 0
Izx = 1.0106e-007	Izy = 0	Izz = 3.7275e-005

Mass Properties for Frame 3 (fingertip frame) with fingertip pressure pad

Output coordinate System: F3 (opaque)

Mass = 0.04166 kilograms

Volume = 1.5911e-005 cubic meters

Surface area = 0.02168 square meters

Center of mass (meters):

X = 0.02295 Y = 0.0010739 Z = 0.00041752

Principal axes of inertia and principal moments of inertia (kilograms * square meters), taken at the center of mass:

Ix = (-0.99919, -0.032581, 0.023483)	Px = 3.0982e-006
Iy = (0.023724, -0.0070039, 0.99969)	Py = 1.5816e-005
Iz = (-0.032406, 0.99944, 0.0077712)	Pz = 1.6962e-005

Moments of inertia (kilograms * square meters), taken at the center of mass and aligned with the output coordinate system:

Lxx = 3.1199e-006	Lxy = 4.5115e-007	Lxz = -2.9813e-007
Lyx = 4.5115e-007	Lyy = 1.6948e-005	Lyz = -1.8635e-008
Lzx = -2.9813e-007	Lzy = -1.8635e-008	Lzz = 1.5809e-005

Moments of inertia (kilograms * square meters), taken at the output coordinate system:

Ixx = 3.1752e-006	Ixy = 1.4779e-006	Ixz = 1.0106e-007
Iyx = 1.4779e-006	Iyy = 3.8897e-005	Iyz = 0
Izx = 1.0106e-007	Izy = 0	Izz = 3.78e-005